אני מדברת רבות על החשיבות של חקר במתמטיקה.
מבחינתי זו הדרך המיטבית ביותר לייצר למידה משמעותית, כזו שמעניינת את התלמידים, יוצרת אצלם הבנה מעמיקה ויותר מהכל מייצרת להם תפיסה חיובית על המתמטיקה.
והיום החלטתי לשתף אתכם בדוגמא קיימת של המורה יפעת.
חשוב שתקראו את כל המאמר ובמיוחד את הנקודות המשמעותיות בסוף שיכולות לסייע לכל מורה ליישם זאת.
יפעת מלמדת בתיכון בדרום הארץ. אני מלווה אותה ואת הצוות שלה כבר למעלה משנתיים בתוכנית ליווי צמודה. ואותה אני מכירה באופן אישי כסטודנטית שלי בתכנית ההסבה במכללה שבה אני מרצה.
מטרת התכנית שיצרנו לבית הספר היא לקדם את המתמטיקה הן בהיבט הלימודי והן בהיבט המנטלי.
הצוות רצה פרקטיקות יישומיות איך לאפשר למתמטיקה להיות יותר מעניינת ומגוונת ואיך להוריד את מפלס החרדה והלחץ מהמקצוע.
לשמחתי השילוב של השניים הוא המומחיות שלי 🙂
הקדשנו מספר מפגשים ללימוד של פדגוגיות חקר ומשימות ביצוע במתמטיקה דרך הוראה דיפרנציאלית. כלומר לייצר הוראה שהתלמידים פעילים, יוצרים וחוקרים בעצמם את המתמטיקה אך בסגנונות למידה שונים, דרך תנועה, ויזואליזציה, הקשבה ועוד.
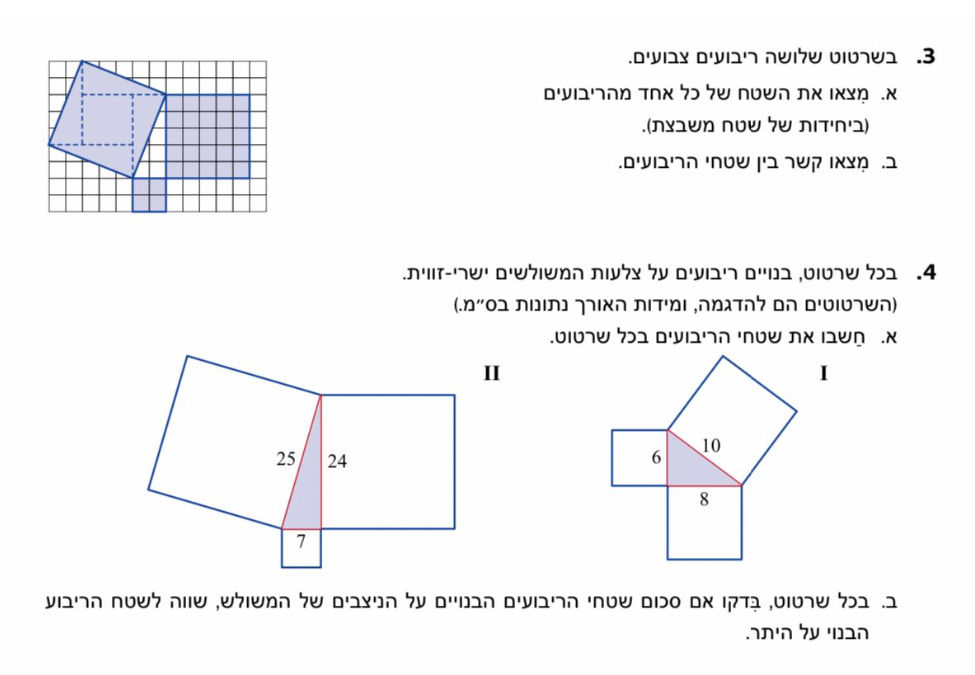
יפעת שמלמדת בכיתות ח' התחילה ללמד את משפט פיתגורס.
נושא, שאיך נאמר, דיי טכני ושטחי עבור מרבית התלמידים.
זו הייתה הזדמנות נהדרת עבורי לייצר עם יפעת שיעור חוויתי כזה שימחיש לתלמידים את היופי שבמשפט ואיך הוא בכלל סייע לאנשים לפני אלפי שנים ויכול לסייע לנו היום.
מהלך השיעור- לפניכם מהלך של הטמעת הפדגוגיה למשימות חקר
שלב 1 חקר עצמי:
זהו חלק משמעותי שבו התלמידים הם הפעילים והחוקרים. הם קיבלו דף עבודה והיו צריכים לחקור לפי הנחיות את הצלעות של הריבוע ולבחון את הקשר ביניהן.

שלב 2 הבנה דרך התנסות וגילוי:
זהו השלב הכי כיפי. כל הילדים (וגם אנחנו המבוגרים 🙂 ) אוהבים לשחק. אז החלטנו לתת לתלמידים להיות חוקרים דרך פעילות משחקית וחוויתית.
החלטנו לתת להם לבחון את נכונות משפט פיתגורס דרך היטלי הצל של עצמם.
תלמידים שסיימו את השלב הראשון יצאו החוצה ובאמצעות מטר מדדו את שלושת האורכים:
*הגובה שלהם
*אורך הצל שלהם
*המרחק בין קודקוד הראש וקודקוד הצל.
(ד"א זה בסיס נהדר לשיעור על דמיון משולשים, יחס, חישוב זוויות בטריגו' ועוד).
לאחר מכן, הם בדקו את נכונות של משפט פיתגורס דרך הצבת כל הגורמים במיקום בנוסחה.
והפלא ופלא המשוואה התבררה כנכונה גם בחיים עצמם 🙂
ובלי קשר לא משנה מתי ואיפה, בכל מקום שבו שני ניצבים יפגשו, משפט פיתגורס ימשיך להתקיים וזו העוצמה המדהימה של הוכחות מתמטיות.

שלב 3 לימוד פורמלי:
כאן מתחיל השיעור הרגיל שכולנו מכירים. הצגת הנוסחה, שמות הגורמים השונים (ניצב ויתר) ושם הנוסחה. אבל בשלב הזה התלמידים כבר התחברו למשפט, לנכונות שלו ולכן הם כבר היו רתומים לתהליך הלמידה.
שלב 4 תרגול:
זהו, מכאן זה רק תרגול שיטתי וחוזר. שימוש בנוסחה בוריאציות שונות (נעלמים, צורות גיאומטריות וכו').
שימו לב כי בדרך כלל הלימוד המסורתי מדלג על שני השלבים הקריטיים בהתחלה וכך מייצר למידה טכנית. אך מספיק שיעור אחד לחקר ולהתנסות פעילה של התלמידים בכדי לגרום להם עניין, סקרנות והירתמות ללמידה.
חששות התנגדויות וטיפים שיכולים לעזור (!!)
אני רוצה לשתף אתכם שהרבה מורים בתוכניות הליווי שלי מעידים על הקושי של הכנסת חקר בכיתות שלהם. הלחץ מהבגרויות, הספק החומר וחוסר הירתמות של התלמידים פשוט מכניע את המורים מלקדם שיעורים כאלו. ואני ממש מבינה ומכירה זאת מניסיון אישי כמורה.
אז הנה כמה דרכים לסייע לכם:
1. תתחילו מדברים קטנים- לא חייב לעשות הפקה של שיעור. זה אמור להיות משהו קל ופשוט עבורכם. אחרי שתחוו חוויה חיובית, רמת הסיפוק שלכם צעלה ותקדם אתכם לעוד שיעור כזה ועוד אחד ועד מהרה תראו שאתם רק מחכים לשיעורים כאלו.
2. הטרמה- שיעור חקר הוא לא שיעור רגיל והתלמידים לא נחשפים אליו. יהיה כאן רעש ובלאגן, תזוזות בשיעור ואולי גם מידה מסויימת של היפרקטיביות . אבל זה לגמרי יכול להיות במינון נמוך יותר אם תעשו הטרמה לתלמידים. כלומר תכינו את התלמידים שהולך להיות שיעור אחר. אם צריך חלוקה לקבוצות אז חלקו אותם מבעוד מועד. הסבירו והנחו כל שלב בשיעור ותסבירו לתלמידים מה מצופה מהם.
3. הערכה- שיעור חקר יכול להיות הזדמנות נהדרת עבורכם לבדוק את הידע של התלמידים ולכן היעזרו בשיעור כזה כתחליף למבדק. הציגו לתלמידים את מדדי הערכה ולפי מה יהיה מורכב הציון שיתקבל מתוך משימות השיעור.
4. ניהול זמן- שיעורי חקר דורשים לרוב יותר זמן. ולכן עדיף לקיים אותו בתחילה/אמצע של יום כאשר יש שעתיים רצופות של למידה.
5. מטרה ברורה- לשיעור חקר צריכה להיות מטרה ברורה של מה אתם רוצים שהתלמידים יחקרו וילמדו. יש המון רעיונות לפעילויות ברשת אבל תזכרו שהחקר אמור לקדם מטרה לימודית ולא ההפך ולכן חשבו קודם כל מה המטרה שלכם בשיעור כזה ולאחר מכן התאימו את משימת החקר.
6. שיבוץ משימות החקר בתכנון החודשי- משימות חקר משולבות עם שיעורי התרגול, ההמלצה שזה יהיה 50% לפחות מהשיעורים שלכם. זה לא תמיד ריאלי. לכן התחילו עם נושאים שאתם אוהבים ללמד והחליטו מבעוד מועד מתי ואיך לשלב את שיעורי החקר בתכנון החודשי שלכם.
והנה התגובה של יפעת מהשיעור שלה. וזה רק מוכיח כמה אפקט חיובי ועוצמתי יש לשיעורים כאלו עבורה ועבור תלמידיה.

